Michaelis–Menten kinetics

Michaelis–Menten kinetics (occasionally also referred to as Michaelis–Menten–Henri kinetics) approximately describes the kinetics of many enzymes. It is named after Leonor Michaelis and Maud Menten. This kinetic model is relevant to situations where very simple kinetics can be assumed, (i.e. there is no intermediate or product inhibition, and there is no allostericity or cooperativity). More complex models exist for the cases where the assumptions of Michaelis–Menten kinetics are no longer appropriate.
The Michaelis–Menten equation relates the initial reaction rate v0 to the substrate concentration [S]. The corresponding graph is a rectangular hyperbolic function; the maximum rate is described as vmax (asymptote).
The Michaelis–Menten equation describes the rates of irreversible reactions. A steady state solution for a chemical equilibrium modeled with Michaelis–Menten kinetics can be obtained with the Goldbeter–Koshland equation.
Contents |
Equation
The validity of the following derivation rests on the reaction scheme given below and two key assumptions: that the total enzyme concentration and the concentration of the intermediate complex do not change over time. The most convenient derivation of the Michaelis–Menten equation, described by Briggs and Haldane, is obtained as follows (Note that often the experimental parameter kcat is used but in this simple case it is equal to the kinetic parameter k2):
The enzymatic reaction is assumed to be irreversible, and the product does not bind to the enzyme.
The first key assumption in this derivation is the quasi-steady-state assumption (or pseudo-steady-state hypothesis), namely that the concentration of the substrate-bound enzyme ([ES]) changes much more slowly than those of the product ([P]) and substrate ([S]). This allows us to set the rate of change of [ES] to zero and also write down the rate of product formation:
The second key assumption is that the total enzyme concentration ([E]0) does not change over time, thus we can write the total concentration of enzyme [E]0 as the sum of the free enzyme in solution [E] and that which is bound to the substrate [ES]:
Substituting this into equation (2), we obtain an expression for [ES] which in turn we can use in equation (3) to find an expression for the rate of product formation:
Because the concentration of substrate changes as the reaction takes place, the initial reaction rate v0 is used to simplify analysis, taking the initial concentration of substrate as [S]. The equation for the reaction rate (4) can also be rewritten in equation (5) which uses the inverse of v0 and [S]. This makes it easier to determine the constants from measured data (a procedure that results in a Lineweaver–Burk plot or a Hanes–Woolf plot).

Equation (4) results in a so called saturation curve which can be observed in the graph on the right. Several interesting cases can be distinguished mathematically and graphically:
- If
![[S]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/38bd6c19740e43396bd14b1575d58f60.png) is large compared to
is large compared to  then the term
then the term ![[S] / (K_M + [S]) \approx 1](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/28e4c03f3a5d506f57d840142edc5cbd.png) . Therefore, the rate of product formation is
. Therefore, the rate of product formation is
-
- Thus the product formation rate only depends on the enzyme concentration, the equation resembles a unimolecular reaction with a corresponding pseudo-first order rate constant k2. Thus it only matters how fast the [ES] complex turns its bound substrate into product and not how often the enzyme and the substrate meet.
- If
![[S] = K_M](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d46898e3cbb3af01ef9b76e74621ef96.png) then
then ![[S] / (K_M + [S]) = [S] / (2[S]) = \frac{1}{2}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/dd0ac694b3754afdb020150aa7f1ea94.png) . Therefore, the rate of product formation is
. Therefore, the rate of product formation is
- If
![[S]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/38bd6c19740e43396bd14b1575d58f60.png) is small compared to
is small compared to  then the term
then the term ![[S] / (K_M + [S]) \approx [S] / K_M](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/7071e21a580398420d8e6bd0673ea3df.png) and also very little ES complex is formed, thus
and also very little ES complex is formed, thus ![[E]_0 \approx [E]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/0f92ba855b6682e83c7195e3899887be.png) . Therefore, the rate of product formation is
. Therefore, the rate of product formation is
-
- Thus the product formation rate depends on the enzyme concentration as well as on the substrate concentration, the equation resembles a bimolecular reaction with a corresponding pseudo-second order rate constant k2/KM. This constant is a measure of how efficiently an enzyme converts a substrate into product. The most efficient enzymes reach a k2/KM in the range of 108 – 1010 M−1 s−1 which is the diffusion limit. These enzymes are so efficient they effectively catalyze a reaction each time they encounter a substrate molecule and have thus reached an upper theoretical limit for efficiency, thus these enzymes have often be termed as perfect enzymes.[1]
Determination of constants

To determine the maximum rate of an enzyme-mediated reaction, a series of experiments is carried out with varying substrate concentrations ([S]) and the initial rate of product formation is measured. 'Initial' here is taken to mean that the reaction rate is measured after a relatively short time period, during which complex builds up but the substrate concentration remains approximately constant and the quasi-steady-state assumption will hold.[2] The measurements can then be plotted in a Lineweaver–Burk plot, plotting the inverse of substrate concentration against the inverse of the initial velocity
The values of the desired constants KM and Vmax can be read directly off the plot. Accurate values for KM and Vmax can only be determined by non-linear regression of Michaelis-Menten data.[3] The inverse plot, while useful for visualization, should never be the source of the actual value of the enzyme constant due to large insensitivity to errors inherent in all inverse plots. Should one need to derive a value from an inverse plot, the Hanes-Woolf plot is the most accurate.[3]
Michaelis constant KM
The reaction rate V is the number of reactions per second catalyzed per mole of the enzyme. The reaction rate increases with increasing substrate concentration [S], asymptotically approaching the maximum rate Vmax. There is therefore no clearly-defined substrate concentration at which the enzyme can be said to be saturated with substrate. A more appropriate measure to characterize an enzyme is the substrate concentration at which the reaction rate reaches half of its maximum value (Vmax/2). This concentration can be shown to be equal to the Michaelis constant (KM); see the section above for a derivation.
For enzymatic reactions which exhibit simple Michaelis–Menten kinetics, the Michaelis constant is defined as (this result comes directly from the derivation of the equation):
Note that the unit of k−1 and k2 is time-1, while the unit of k1 is concentration-1 times time-1. This can be seen from eq. (2) above, since k1 is multiplied by the product of two concentrations ([E] times [S]) but k−1 and k2 are multiplied by a single concentration ([ES]). For example, if the unit of concentration is millimolars (mM) and the unit of time is seconds, the unit of k−1 and k2 is sec-1 and the unit of k1 is mM-1sec-1. Thus the unit of KM in the equation above is "concentration", or in this example, mM.
In the most simple case, when product formation is the rate-limiting step (i.e. when k2 << k−1) the constant will just be equal to the dissociation constant (affinity for substrate) of the enzyme-substrate (ES) complex
However, often k2 >> k−1, or k2 and k−1 are comparable, in which case there will be significant contributions to KM in addition to the affinity of the enzyme for the substrate.[4]
Limitations
The first source of limitations for the Michaelis-Menten kinetics is that it is an approximation of the kinetics derived by the law of mass action. In particular, Michaelis-Menten kinetics is based on the quasi-steady state assumption that [ES] does not change,
which is only approximately true: the rate of change of the complex [ES] is very small but non-zero. The quality of the approximation depends on the timescale separation present in the dynamics on the phase space, which controls the magnitude of the rate of change of [ES]. In particular, it has been shown[5] that this timescale separation is measured by a small, positive parameter,
where S0 is the initial concentration of the substrate and E0 and KM have been defined above. The smaller 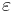 is, the larger the timescale separation present in the system and the more accurate is the quasi-steady state approximation.
is, the larger the timescale separation present in the system and the more accurate is the quasi-steady state approximation.
The second limitation is that Michaelis–Menten kinetics relies upon the law of mass action which is derived from the assumptions of free (Fickian) diffusion and thermodynamically-driven random collision. However, many biochemical or cellular processes deviate significantly from such conditions. For example, the cytoplasm inside a cell behaves more like a gel than a freely flowable or watery liquid, due to the very high concentration of protein (up to ~400 mg/mL) and other “solutes”, which can severely limit molecular movements (e.g., diffusion or collision)[6]. This causes macromolecular crowding, which can alter reaction rates and dissociation constants.[7][8]
For heterogeneous enzymatic reactions, such as those of membrane enzymes, molecular mobility of the enzyme or substrates can also be severely restricted, due to the immobilization or phase-separation of the reactants. For some homogeneous enzymatic reactions, the mobility of the enzyme or substrate may also be limited, such as the case of DNA polymerase where the enzyme moves along a chained substrate, rather than having a three-dimensional freedom. The limitation on molecular mobility (as well as other “non-ideal” conditions) demands modifications on the conventional mass-action laws, and Michaelis–Menten kinetics, to better reflect certain real world situations. Although it has been shown that the law of mass action can be valid in heterogeneous environments (see, R. Grima and S. Schnell [9]). In general physics and chemistry, limited mobility-derived kinetics have been successfully described by the fractal-like kinetics. R. Kopelman [10], M.A. Savageau [11], and S. Schnell [12] pioneered the “fractal enzymology”, which has been further developed by other researchers.[13]
See also
Notes
- ↑ Stroppolo ME, Falconi M, Caccuri AM, Desideri A (2001). "Superefficient enzymes". Cell. Mol. Life Sci. 58 (10): 1451–60. doi:10.1007/PL00000788. PMID 11693526.
- ↑ Segel L.A. and Slemrod M. (1989). "The quasi-steady-state assumption: A case study in perturbation". SIAM Review 31: 446–477. doi:10.1137/1031091. http://siamdl.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=SIREAD000031000003000446000001&idtype=cvips&gifs=Yes.
- ↑ 3.0 3.1 Leskovac V. (2003). Comprehensive Enzyme Kinetics..[1]
- ↑ Nelson, DL., Cox, MM. (2000) Lehninger Principles of Biochemistry, 3rd Ed., Worth Publishers, USA
- ↑ Segel L.A. and Slemrod M. (1989). "The quasi-steady-state assumption: A case study in perturbation". SIAM Review 31: 446–477. doi:10.1137/1031091. http://siamdl.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=SIREAD000031000003000446000001&idtype=cvips&gifs=Yes.
- ↑ Olsen S. (2006). "Applications of isothermal titration calorimetry to measure enzyme kinetics and activity in complex solutions". Thermochim. Acta 448: 12–18. doi:10.1016/j.tca.2006.06.019..[2]
- ↑ Zhou HX, Rivas G, Minton AP (2008). "Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences". Annu Rev Biophys 37: 375–97. doi:10.1146/annurev.biophys.37.032807.125817. PMID 18573087.
- ↑ Minton AP (2001). "The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media". J. Biol. Chem. 276 (14): 10577–80. doi:10.1074/jbc. R100005200. PMID 11279227. http://www.jbc.org/cgi/content/full/276/14/10577.
- ↑ Grima R., Schnell S. (2007). "A systematic investigation of the rate laws valid in intracellular environments.". Biophys. Chem. 124: 1–10. doi:10.1016/j.bpc.2006.04.019.
- ↑ Kopelman R. (1988). "Fractal reaction kinetics.". Science 241: 1620–1626. doi:10.1126/science.241.4873.1620. http://www.sciencemag.org/cgi/reprint/241/4873/1620.pdf.
- ↑ Savageau M.A. (1995). "Michaelis–Menten mechanism reconsidered: Implications of fractal kinetics.". J. Theor. Biol. 176: 115–124. doi:10.1006/jtbi.1995.0181. http://www.sciencedirect.com/science?_ob=MImg&_imagekey=B6T2K-3WH53P4-2-5P&_cdi=4921&_user=2009156&_orig=search&_coverDate=06%2F07%2F1998&_sk=999529998&view=c&wchp=dGLbVtb-zSkWA&md5=98198068127ec65569c44f2ba3daa223&ie=/sdarticle.pdf.
- ↑ Schnell S. and Turner T.E. (2004). "Reaction kinetics in intracellular environments with macromolecular crowding: simulations and rate laws.". Prog. Biophys. Mol. Biol. 85: 235–260. doi:10.1016/j.pbiomolbio.2004.01.012.
- ↑ F. Xu and H. Ding (2007). "A new kinetic model for heterogeneous (or spatially confined) enzymatic catalysis: Contributions from the fractal and jamming (overcrowding) effects.". Appl. Catal. A Gen. 317: 70–81. doi:10.1016/j.apcata.2006.10.014. http://www.sciencedirect.com/science?_ob=MImg&_imagekey=B6TF5-4MD465X-1-T&_cdi=5217&_user=2009156&_orig=search&_coverDate=01%2F27%2F2007&_sk=996829998&view=c&wchp=dGLbVzz-zSkzV&md5=b1717d5bce455e248254870b420910e4&ie=/sdarticle.pdf.
Further reading
 Biochemistry/Catalysis at Wikibooks.
Biochemistry/Catalysis at Wikibooks.
External links
- Enzyme assay development and analysis
- LMMpro, a Michaelis–Menten optimization software
- Real-time model for comparing Michaelis–Menten analysis to numerical analysis
|
|||||||||||
![\begin{align}
v_0 &= \frac{ v_\max {[}S{]}}{K_M + {[}S{]}}
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/f02b03a741bc2269392ab24f710b2715.png)

![\begin{align}
\frac{d{[}ES{]}}{dt} &= k_1{[}E{]}{[}S{]} - {[}ES{]} (k_{-1} + k_2) \; \overset{!} = \;0 \qquad (2) \\
\frac{d{[}P{]}}{dt} &= k_2 {[}ES{]} \qquad (3) \\
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ec76f66dd13a094476debdc69687f59f.png)
![{[}E{]}_0 = {[}E{]} + {[}ES{]} \; \overset{!} = \; \text{const}.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/217c0609fbb3ab79c4378c763f9b935b.png)
![\begin{align}
0 &= k_1{[}S{]}({[}E{]}_0 - {[}ES{]} ) - {[}ES{]} (k_{-1} + k_2) \\
k_1{[}S{]}{[}E{]}_0 &= k_1{[}S{]}{[}ES{]} + {[}ES{]} (k_{-1} + k_2) \\
{[}S{]}{[}E{]}_0 &= {[}S{]}{[}ES{]} + {[}ES{]} \underbrace{\frac{(k_{-1} + k_2) }{k_{1}}}_{K_M}\\
{[}S{]}{[}E{]}_0 &= ( K_M + {[}S{]}) {[}ES{]}\\
{[}ES{]} &= \frac{{[}S{]}{[}E{]}_0}{K_M + {[}S{]}} \\ \\
\frac{d{[}P{]}}{dt} &= v_0 = k_2 {[}ES{]} = \underbrace {k_2 {[}E{]}_0}_{v_\max}\frac{{[}S{]}}{K_M + {[}S{]}}\\
v_0 &= \frac{ v_\max {[}S{]}}{K_M + {[}S{]}} \; \; \; \; \; \qquad \qquad (4) \\ \\
\frac{1}{v_0} &= \frac{K_M}{v_\max} \cdot \frac{1}{{[}S{]}} + \frac{ 1 }{v_\max } \qquad (5)
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/650768045730b14909412c3502a8e299.png)
![\frac{d{[}P{]}}{dt} \approx v_\max = k_2 [E]_0](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/1737c03d8943136b9bd50678a8393dc0.png)
![\frac{d{[}P{]}}{dt} = 0.5 \cdot v_\max = 0.5 \cdot k_2 [E]_0](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/653076eec5edb4b0412a1379dd34d765.png)
![\frac{d{[}P{]}}{dt} \approx v_\max \cdot [S] / K_M \approx \frac{k_2}{K_M} [E] [S]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/925fe4693268aa4c6b88f22cf8230096.png)
![\frac{1}{v_0} = \frac{K_M + [S]}{V_\max [S]} = \frac{K_M}{V_\max} \cdot \frac{1}{ [S]} + \frac{1}{V_\max}.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/81a68a64a3548fcef246c025ab537994.png)

![K_M \approx \frac{k_{-1}}{k_1} = \frac{[E] [S]}{[ES]} = K_d.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/4157c175806d4254b4f17bb9d891ccb0.png)
![\frac{d[ES]}{dt} = 0 ,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/378df11b3c3c2365228c3933b04a8d4e.png)
